First Order Differential Equations: quick guide

Types of First order ordinary differential equations:

Matrices (a cheat sheet)

Vector algebra (a cheat sheet)

Vectors and Vector spaces

A linear vector space is a set V that is closed under finite vector addition and scalar multiplication.

By closed we mean that after finite vector addition and (or) scalar multiplication of any number of vectors belonging to that space, the result is a vector that also belongs to that space.
e.g. we can say that the set of integers (whole numbers) is closed under addition because the sum of any two of them is also an integer (2+45 = 47, 4+(-2) = 2 etc.) However, it is not closed under division because you can find a pair whose division is a fraction (e.g. 2/3, -3/5 etc.).

Formally, a nonempty set V (of vectors), each with the same number of components such that:

1. If a vector¹  a is an element of V), so is αa, where α is a scalar (we’ll take the set of real numbers as acceptable values for α here for simplicity, i.e. we assume that α ∈ R).
   If a ∈ V ⇒ αa ∈ V
2. If there are two vectors a and b, both elements of V and two scalars α and β, both real numbers then αa + βb is also an element of V
   i.e. if a, b ∈ V and α ,β ∈ R, then αa + βb ∈ V
   and
   α(a + b) = αa + αb
   α(βa) = (αβ)a
   (α + β) = αa + βb
3. Vector addition is commutative
   a + b = b + a ,
   (a + b) + c = a + (b + c)
4. There exists an identity element for addition 0
   a+0 = 0 + a
   where 0 is called the Null vector which is defined to be a vector with zero length (and no direction).
5. For every vector a in V, there exists another vector –a in V such that
   a + (-a) = (-a) + a = 0
6. There exists an identity element of multiplication 1
   1a = a

Linear Combination of Vectors

A weighted combination of vectors a, b, c etc. (all belonging to V) is called a linear combination of them(r,s,t etc. are real numbers here):

v = ra + sb + tc +…

If this sum is zero, i.e.

v = 0 = ra + sb + tc +…

such that all coefficients r,s,t etc have to be zero separately; then the vectors a, b, c etc. are said to be linearly independent. Otherwise they are called linearly dependent. If they are linearly independent, none of them can be expressed as the weighted sum of the rest.

Let’s understand it with the help of an example. Suppose we have three vectors such that

Then we can write   as a combination of  and   :

Or alternatively we can write  in terms of  and   :

Hence, the vectors  ,  and  are linearly dependent. However, if we have another three vectors ,  , such that

Then there is no way to express any one of them as a linear combination of the other two. Hence, they are said to be linearly independent.

If the given vectors are linearly independent such that every other vector in that space can be expressed as a linear combination of them, they are said to be basis vectors.

A Basis is a linearly independent subset of V, consisting of the maximum possible number of vectors. When a vector is expressed as a linear combination of basis vectors, the coefficients multiplying the basis are called components of that vector relative to that basis.

e.g. the vector   encountered before was expressed in terms of cartesian unit vector basis:

here the components are (0, 2, 1) respectively, corresponding to  , and .

The maximum number of linearly independent vectors in V is called the dimension of V. The familiar cartesian coordinate space is a 3-dimensional space (one of the basis set being unit vectors , and  ).

The set of all linear combinations of given vectors with the same no. of components is called the Span of these vectors. Span of a bunch of vectors is a vector space in itself.

Subspace

A subspace of V is a nonempty subset of V that forms another vector space V’ with respect to the two algebraic operations (addition and scalar multiplication) defined for the vectors in V.

Subspace S is orthogonal to another subspace  if every vector in S is perpendicular to every vector in T.

Orthogonality and Norm

It is important to understand that the concept of vectors goes deeper than a quantity having certain magnitude and direction. It is not necessary for a vector to have only 3 components. There are vectors encountered in physics that have no direction in the traditional sense of the word, and has more than 3 components. In those cases, we express vectors simply by components relative to a given basis. In fact, vectors are best expressed in terms of matrices. The concept of orthogonality is then expressed in terms of inner products between row and column matrix representation of vectors and there is no way we can visualize them being ‘perpendicular’ to each other:

 and  are said to be orthogonal if

The concept of length of the vector is then replaced by ‘norm’. In simple terms, norm of a vector is the (modulus of) square root of the inner product of a vector with itself:

The null vector  has been assigned the norm of length zero.

¹I have used both bold letters (such as a) and arrow notation (such as  ) to denote vectors in this post. In the printed text bold letter notation is generally preferred, but the arrow notation helps you recognize a vector quickly and cannot be confused with emphasized text(also in bold) in my opinion.

Scalars and Vectors

Scalar: A quantity that has only one property: magnitude (or value). For example, the temperature only needs to be specified in terms of its value, such as 350 K or 25 ºC, etc.

Vector: A quantity that has two properties; magnitude and direction. For example, 30 km/h to the West is velocity, a vector quantity.

Watch the video below to learn more (credits-TED-Ed):

Actually, both scalars and vectors are special cases of a general class of quantities, known as tensors. You can understand them in terms of multidimensional arrays, if you are familiar with programming. But if you want an intuitive explanation, watch the excellent video by Dan Fleisch:

More on vectors and vector spaces in a future post.

Chance and Probability

Chance: the likelihood of something happening, based on a guess.
Usually, if the probability of an event is greater than 5%, it is considered to have a chance of happening.
e.g. there is a chance it might rain today because I see clouds in the sky.

Probability: the quantified likelihood of something happening out of all the possibilities, based on the average behavior of the experiment in question.
e.g. there is 50% probability that you’ll get heads in the toss of an unbiased coin. It is about accurately estimating the odds of something happening.

Now by 50% chance I don’t mean that if you toss a coin twenty times you’ll get heads 10 times and tails 10 times, in fact that rarely happens. But your results will be close to 10, i.e. you might get heads 11 times and tails 9 times or, heads 8 times and tails 12 times.
Mathematically, we say that if you repeat this experiment infinite (read very large) number of times, about 50% of the times you’ll get heads. It may not be exactly 50%, but it will be close to it.

Trigonometry: Angles

Trigonometry = Trigo (from triangle) + Metry (to measure)

Angles

Angles are a measure of rotation of a given ray about its initial point (the vertex).

Degrees

Degree is a unit for angle measurement.

1 degree = 60 minutes = 3600 seconds

e.g. 36° 40′
= 36+(40/60)
= 36 + 0.67
= 36.67°

Degrees and Radian

1 complete revolution = 360° = 2π Radian

More useful formulae:

That is it for today.
For more, see my notes on Trigonometric Functions here.

Relations and Functions

The set theory helps us understand how a collection of like objects behave. Venn diagrams are useful when you have different sets of the same type. However, to work with sets of different kinds, you need to know the concept of relations and functions.

Suppose your are given two sets, A and B such that

A = {a,b,d,k, j,v} and
B = {Anu, Ben, Don, Kaushik, Sonia}

We can define another set R such that

R = {(x,y) : x is the first letter in the word y; x ∈ A and y ∈ B}
= {(a,Anu), (b,Ben), (d,Don), (k,Kaushik)}

Arrow Diagram representation of relation R

Every member of R is an ordered pair such that the first element x is from set A and second element y is from set B. However,not every element of A or B is included.

y is called the image of x.

The set R here, is an example of a relation.
Formally,

Relation R on A and B is a subset of A x B,

where A x B is the Cartesian product of sets A and B. 

Cartesian Product of Sets

The cartesian product A x B is the set of ordered pairs (a,b) such that a is an element of A and b is an element of B. In the given example, the Cartesian product A x B will be

A x B = {(a, Anu), (a, Ben), (a, Don), (a, Kaushik), (a, Sonia), (b, Anu), (b, Ben), (b, Don), (b, Kaushik),               (b, Sonia), (d, Anu), (d, Ben), (d, Don), (d, Kaushik), (d, Sonia), (k, Anu), (k, Ben), (k, Don), (k,                Kaushik), (k, Sonia), (j, Anu), (j, Ben), (j, Don), (j, Kaushik), (j, Sonia), (v, Anu), (v, Ben), (v,                    Don), (v, Kaushik), (v, Sonia)}
n(A x B) = n(A) x n(B)
= a x b = 6 x 5 = 30

R ⊆ A x B

We know that the number of subsets of a set containing n elements = 2^n
Since R ⊆ A x B,
hence the total number of relations that can be defined on A and B = 2^ab

Some useful properties involving Cartesian product:

A x (B∩C)  = (A x B) ∩ (A x C)
A x (B∪C)  = (A x B) ∪ (A x C)

Domain and Range

For any relation R defined on A and B, we can define the domain and range as:

Domain of R is the set of all first elements, {x} of the ordered pairs (x,y).

In the above example, domain of R = {a,b,d,k}

Range of R is the set of all second elements, {y} of the ordered pairs (x,y).

In the above example, range of R = {Anu, Ben, Don, Kaushik}

The set B, is called the codomain of R.
In the above example, codomain of R = {Anu, Ben, Don, Kaushik, Sonia}

Clearly,

Range ⊆ Codomain

That is it for today. 

Part 2: Venn Diagrams and operations on Sets

For introduction to set theory, see part 1 here

To continue our discussion, let’s study Venn diagrams. These are very helpful way to visualize set operations.
Let’s start with an example:

Let there be two sets A and B such that

A = {x:x is a perfect square and x ≤ 25} = {1, 4,9,16,25}
B = {y: y is an even number and y < 25} = {2,4,6,8,…,24}

We can depict this data in the form of a Venn Diagram as follows:

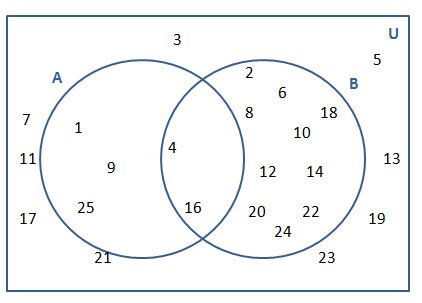
Sets are represented as circles and members are written inside of their set. Members which are common to both sets are written at the common area between the circles.
Note that the universal set U is denoted by the rectangle (here can be taken as the set of all numbers from 1 to 25).

Set operations: Union

Union of two given sets, A and B, is defined as the set which contains members of either A or B or both. It is denoted as A ∪ B.
Taking the above example,
A ∪ B = {1, 2, 4, 6, 8, 9, 10, 12, 14, 16, 18, 20, 22, 24, 25}

Set operations: Intersection

Intersection of two given sets, A and B, is defined as the set which contains members which are common to both A and B. It is denoted as A ∩ B.
Taking the above example,
A ∩ B = {4, 9, 25}

Set operations: Difference

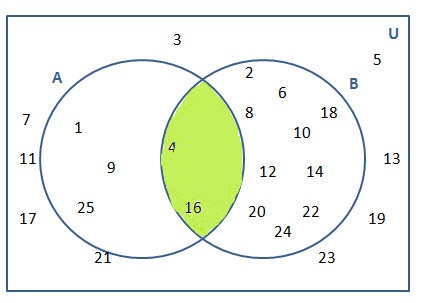
Difference of two given sets, A and B, is defined as the set which contains members which belong to A, but not to B. It is denoted as A–B.
Again, taking the above example,
A–B = {1, 9, 25}

Set operations: Complement

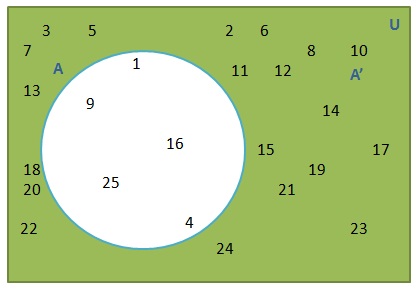
Complement of a given set A, is denoted by A′ and is defined as the set which contains members which belong to U, but not to A.
It can be easily verified that, A′= U–A.
Again, taking the above example,
A′= U–A = {2,3,5,6,7,8,10,11,12,13,14,15,17,18,19,20,21,22,23,24}

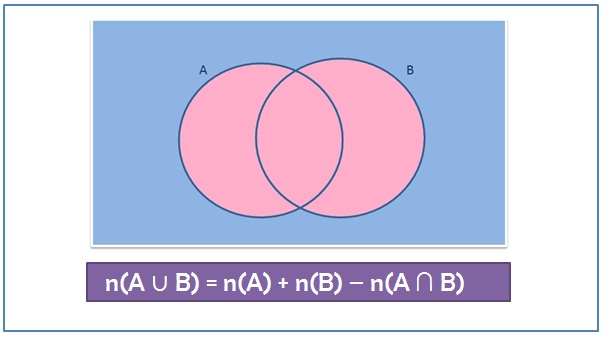
A very useful relation in set theory is

n(A∪B)  =   n(A) + n(B) – n(A∩B)
i.e., total no.of elements in A and B = no. of elements in A + no. of elements in B – no. of elements in both A and B

(because when we count no. of elements in A+no. of elements in B, we counted common elements twice, hence we subtract them once from total)

There are a couple of useful properties, known as the De Morgan’s laws:

That is it for set theory.

Part 1: The Set Theory (basics)

Sets

Our solar system has 8 planets: Mercury, Venus, Earth, Mars, Jupiter, Saturn, Neptune and Uranus. They all have one feature in common: they  are relatively big round objects that revolve around the Sun. We all have agreed upon this identification and no other object can be said to be a planet of our solar system (sorry Pluto).

Such a collection of well-defined objects is called a set. Note that the members (or elements) of a set have at least one common property that is not shared by anything that is not included in that set.

Sets are denoted by capital letters and the elements are listed inside curly braces as shown in the following examples:

The empty set

A set which contains no element. Denoted by Φ or {}.

e.g.
A = {x: x is a natural number such that 3<x<4}
since no such number exists, A is an empty set.

Finite and infinite sets

A set with countable elements is called a finite set.
A set with infinite number of elements is called an infinite set.

e.g.
The set of vowels, V = {a,e,i,o,u} is a finite set.
The set of natural numbers, N = {1,2,3…} is an infinite set.

Equality of sets

Two sets are said to be equal if and only if they have exactly the same elements.
e.g.
A = {1,2,3} and
B = {3,3,2,1}
are equal because the elements of both are the same.

Note that it doesn’t matter if the elements are repeated or written in a different sequence.

Hence,
A = {x : x is a letter in the word “ALLOY”} and
B = {y: y is a letter in the word “LOYAL”}

are equal and we can write
A = B = {A,L,O,Y} = {L,O,A,Y} etc.

Subset

Consider two sets A and B such that

A = {1,2,3,4,5} and
B = {1,2,4}

We see that every element of B is also an element of A. But not every element of A is that of B (for example, 3 belongs to A but not B).

We say that B is a subset of A and A is the superset of B.
Note that every set is a subset of itself. Also, Φ is a subset of every set.

Power set

The collection of all subsets of a set A is called the power set of A. It is denoted by P(A).

e.g. if A = {a,s,d}
then P(A) = {{a},{s},{d},{a,s},{s,d},{a,d},{a,s,d},Φ}.

Universal set

Consider the set of real numbers, R. Every rational or irrational number belongs to the set R. Every integer belongs to R. Calculations in mathematics all deal with numbers that lie within the domain of real numbers (excluding complex analysis, we shall deal with that later). Hence, we get the ‘sense’ that the set of real numbers, R, is a superset of all the sets involving numbers. For our context, the set R is then called the ‘Universal set’.
Another example is the set of countries, if we want to know which of them are members of the UN, we can consider the set of all countries of the world as the universal set.

 

A universal set is one of the supersets of all the sets in a given context (denoted by U). It is usually specified according to the problem at hand.

That is it for today.

For details, see my notes on set theory: set theory-definitions.